Числовые последовательности
Если каждому натуральному числу n поставлено в соответствие некоторое вещественное
число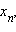 
то
говорят, что задана числовая
последовательность x1, х2, …,
хn =
{xn}
Примеры числовых последовательностей:
2, 4, 6, 8, 10, … , 2n, … ;
1, 4, 9, 16, 25, … , n? , … ;
1, 1/2, 1/3, 1/4, 1/5, … , 1/n , …
|
|
n |
|
2 |
1 |
|
6.7 |
3 |
|
3.100 |
5 |
|
0 |
7 |
Способы задания последовательностей
Последовательности можно задавать различными способами, среди которых особенно
важны три:
аналитический,
описательный
рекуррентный.
1. Последовательность задана аналитически, если задана формула ее n-го
члена:
xn = f(n).
Пример. xn = 2n – 1 – последовательность
нечетных чисел: 1, 3, 5, 7, 9
2. Описательный способ задания числовой последовательности состоит в том,
что объясняется, из каких элементов строится последовательность.
Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о
стационарной последовательности 1, 1, 1, …, 1, ….
Пример 2. «Последовательность состоит из всех простых чисел в порядке
возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При
таком способе задания последовательности в данном примере трудно ответить, чему
равен, скажем, 1000-й элемент последовательности.
3. Рекуррентный способ задания последовательности состоит в том, что указывается
правило, позволяющее вычислить n-й член последовательности, если известны
ее предыдущие члены. Название рекуррентный способ происходит от латинского слова
recurrere – возвращаться. Чаще всего в таких случаях указывают формулу,
позволяющую выразить n-й член последовательности через предыдущие, и
задают 1–2 начальных члена последовательности.
Свойства числовых последовательностей
Числовая последовательность – частный случай числовой функции, поэтому ряд
свойств функций рассматриваются и для последовательностей.
Определение. Последовательность {xn} называют
возрастающей, если каждый ее член (кроме первого) больше предыдущего:
x1 < x2 < x3< … < xn < xn+1 < ….
Определение. Последовательность {yn} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:
x1> x2> x3>
… > xn > xn+1 > … .
Возрастающие и убывающие последовательности объединяют общим термином –
монотонные последовательности.
Если
Числовая последовательность, каждый член которой, начиная со второго,
равен сумме предыдущего члена и одного и того же числа d, то
последовательность называют арифметической прогрессией.
xn = xn-1 + d (n = 2, 3, 4, …)
Где
d- разность арифметической прогрессией
x1 -первый член арифметической прогрессией
xn - общий член арифметической прогрессией
Пример
1, 3, 5, 7, 9, 11-– возрастающая арифметическая прогрессия, у которой
x1 =1 ,d=2
Пример.
20, 17, 14, 11, 8, 5, 2, –1, –4,… – убывающая арифметическая прогрессия, у которой
x1 =20 ,d=-3
Числовая последовательность является арифметической тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.
(
)/2 =xn
Формула n-го члена арифметической прогрессии
xn = x1 + (n-1)*d (n = 1,2, 3, 4, …)
Пример 1
Если дана арифметическая прогрессия
1,3,5,7,9,11.......
членами которой является все последовательные положительные нечетнын числа,то
xn =1+2(n-1)=2n-1
Пример 2
Если x1 =7 и d =3 то
xn =7+3(n-1)=3n+4
Пример 3
Если x1 =10 и d =-0,5 то
xn =10-0,5(n-1)=-0,5n+10,5
Нахождения величин
x1 =xn -d(n-1)
d=(xn -x1)/(n-1)
n=((xn -x1)/d)+1
