TRANSFORMATION
So far, you have learned about 3D objects, the Cartesian coordinate system, and the
difference between object space and world space. LetТs move on and learn how we can use
XYZ values to define an objectТs transformation in addition to its size, shape, and
position.
An objectТs transformation
describes an objectТs
position (translation),
orientation(rotation), and
size (scale) in 3D space.
When an object is first created(когда объект первый раз создан ), its transformation is set to align with the global coordinates.
Its position(translation),
is set center to(устанавливаютс¤ в центре системе координат ) = {0,0,0},
its orientation(rotation,) is set = {0,0,0},
and its size (scale) is set to(и размер(масштаб) установлен) = {1,1,1}.
An objectТs transformation values are almost certain to change as you work with
the object.
Translation
An objectТs translation describes its position in 3D space relative to its center and is
measured in defined grid units. LetТs take another look at the box we used in an earlier
example:
As you can see, the boxТs center is the same as the origin ({0,0,0}). What happens if you
want to move the box? You can move each one of the points, delete the existing box and
draw a new one in its new location, or simply translate the box. For example, setting a
Translate value of {2,2,2} would move boxТs lower left corner to {0,0,0} since (-2)+2=0.
Again, the Translate value refers to the
location of the center of the object relative to world space.
Rotation
An objectТs rotation value refers to its orientation in 3D
space measured in degrees. As you probably know, any
actual object will revolve around its
center of gravity 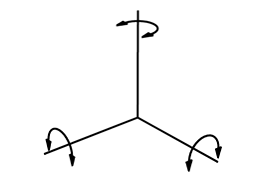
(balance point). Objects in Poser have no mass and no
center of gravity, so you can set the objectТs center
wherever you like and the object will rotate around that
point.
LetТs think back to the motorcycle example. If you model a motorcycle and decide you
wish to lean it 45 degrees, nothing is stopping you from performing trigonometric
calculations to determine the new location of each part. Remember that each part of the
motorcycle will move in at least two dimensions as the whole machine rotates. In this
case, since the motorcycle is rotating about the Z axis, you could simply enter a rotation
value of {0,0,45}. The trigonometric calculations will still need to be performed, however
Poser will get stuck with the job instead of you.
Scale
An objectТs scale value refers to its size in relation to itself and is measured in percent. In
this case, a value of 1 corresponds to 100%. Take the example of a circle. As with all other
Poser objects, it is initially created with a scale value of {1,1,1}, meaning that it is 100%
of its original size in all three dimensions.
Now that your perfect circle is in
place, you realize you need to
double its height on the Y axis.
Simply enter a scale value of
{1,2,1} and the circle will turn into 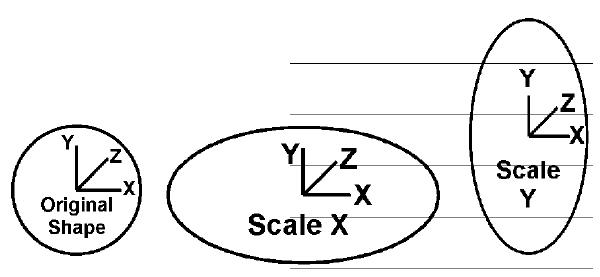
an ellipse that is twice as long on
the Y axis as it is wide. To stretch it
on the X axis, you would enter
{2,1,1}.
To compute every point on a model, multiply the original coordinates by the X, Y, and Z
components. With this in mind, it becomes easy to see how different values can change the
size of your object. For example, entering a scale value of {2,2,2} would double the
circleТs size. Poser allows you to set each scaling factor independently in order to obtain
squashing and stretching effects. This is called differential scaling.