The RMS Voltage of an AC Waveform

The term “RMS” stands for “Root-Mean-Squared

root-mean-square

средняя квадратическая

Алгоритм

 

 

Step 1


The mathematical formulation of the data

 

 

Waveform

 

 

 


Vpp=2Vp=2Um=2Max

 

  

 

  

 

 

 

 

 

 

 

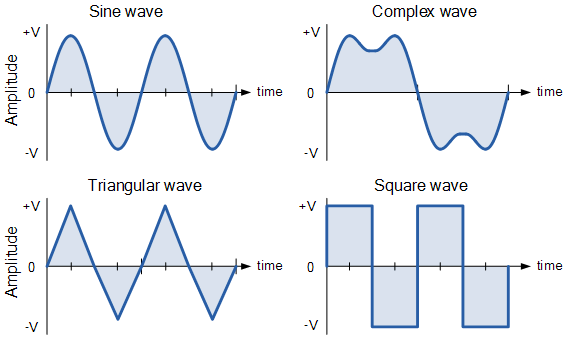
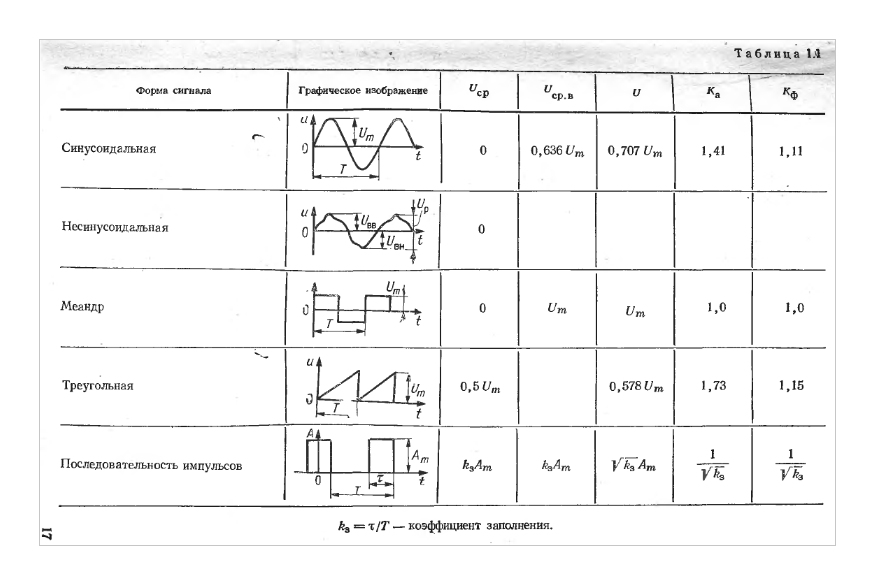
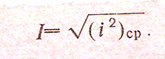
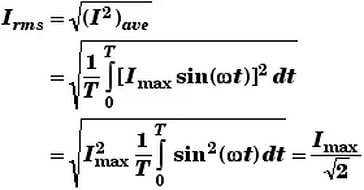
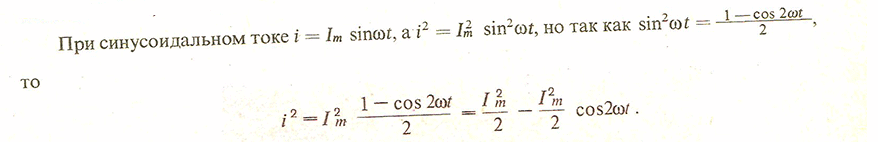
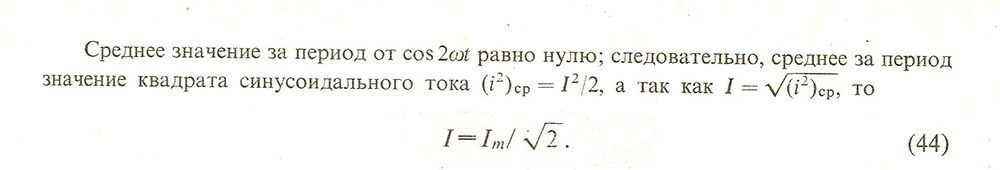
Действующее
значение тока

- среднеквадратичное значение периодического электрического тока. Для синусоидального тока действующее значение тока в √2 раз меньше амплитудного (максимального). Когда без пояснений указывают значение переменного тока, то имеют в виду действующее значение.
 
   На рисунке: I - действующее значение тока,
        i - мгновенное значение тока,
        t - время, T - период,
       Im - амплитудное значение тока.
 
 
♦  Де́йствующее значе́ние то́ка

 

Действующее
значение напряжения

Current the value of the voltage

- среднеквадратичное значение периодического электрического напряжения. Для синусоидального тока действующее значение напряжения в √2 раз меньше максимального (амплитудного). Когда без пояснений указывают значение напряжения переменного тока, то имеют в виду действующее значение.
 
   На рисунке: U - действующее значение напряжения,
        u - мгновенное значение напряжения,
        t - время, T - период,
       Um - амплитудное значение напряжения.
 
 
♦  Де́йствующее значе́ние напряже́ния

root mean square voltage

 

Integrating through with limits taken from 0 to 360o or “T”, the period gives:

rms voltage integration

 

 

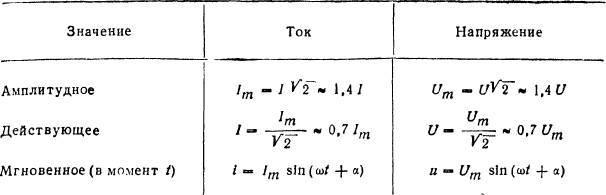
So how do we calculated the RMS Voltage of a sinusoidal waveform. The RMS voltage of a sinusoid or complex waveform can be determined by two basic methods.

8. Среднеквадратичное значение: среднеквадратичное значение напряжения всего сигнала или выбранной области. , где это измеряемая i-я точка, а это количество измеряемых точек.

9. Vrms-1: the root mean square value within a period. The calculation formula is as follows.

21niixRMSn==Σ, wherein, ixis the ith point being measured, nis the number of points being measured.

 

 

Step 2

Verification of theoretical data

Эксперементальные данные

Теоретические данные

Математические данные

Frequency = 20kHz

f := 20

Amplitude  =  2.00Vpp

Vp= Vm=Max = 1.00

DC Offset = 0 mVDC

a=0

Start Phase = 0

 

 

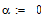Step 3.

Verification  of experimental data

Эксперементальные данные

Frequency = 20kHz

Amplitude  =  2.00Vpp

DC Offset = 0 mVDC

Start Phase = 0

Вводим данные(Смотрим алгоритм)
how to output a Sine waveform in DG1000Z

Измерение переменного напрежения вольтметром(Смотрим алгоритм).

 

Measur   in  oscilloscope

Сравниваем данные

 

   

 

backward