Реальная или вертуальная ? Постоянно в движении.

Информация получена из
Краткий курс математического анализа-А.Ф.Бермант Москва 1966 г.

Векторная функция скалярного аргумента.

Из всего  написанного здесь только линия L является реальной , объективной существующей величиной.
Именно линию L можно наблюдать физически(то что можно видеть реально) в пространстве и во времени.
Все другие величины условные(вертуальные) и служат  для вычисления(определения) линии L.

L=L(t)
 

Движение материальных объектов совершается в пространстве (space)  при изменении времени (time)
Изучением движения точки заключается в

1.положения (position) точки в выбранной системе отсчета
2.скорости (translate)  
3.ускорения в любой момент времени.

 Кривая линии(L) в пространстве и во времени.

Уравнения движения точки  в пространстве и во времени   в декартовых координатах  имееют вид
 

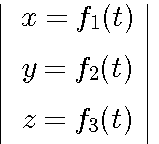
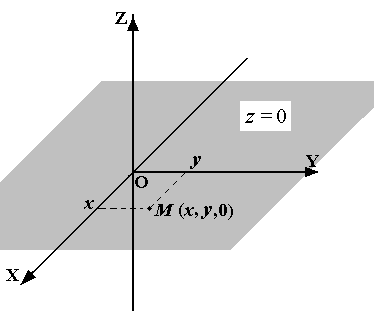
Если точка движется(translate)  в плоскости          xOy, то
                                                                                      

                                                                                                                                      будет только два уравнения движения.
                                        

                                                                                                                                      
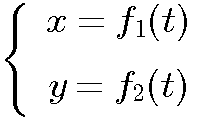
                                                                                                                                        position =vector( x(t), y(t), 0.0000 )

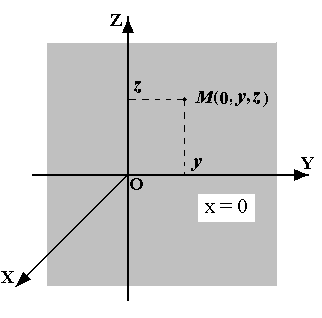
Если точка движется(translate)  в плоскости          yOz,то

                                                                                          

                                                                                                                                    будет только два уравнения движения.

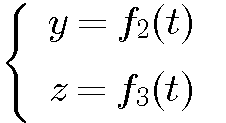
                                                    position=vector( 0.0000,y(t),z(t) )

 
 Если точка движется (translate) в плоскости     xOz   , то

                                                                                                                                                будет только два уравнения движения.

                                                           position=vector( x(t),0.0000,z(t) )

Сущность всей системы
 

Иными словами
Если имеется линия  L=L(t)(график движения)     то её  можно разложить на составляющие векторной системе координат  
x=x(t)
у=x(t)
z=z(t)
r=x(t)i+y(t)j+z(t)k
Практическое применение
 Если требуется создать линию L=L(t)(график движения)  в  векторной системе координат   то её надо составить  из
x=x(t)
у=y(t)
z=z(t)

x(t)i+y(t)j+z(t)k=r