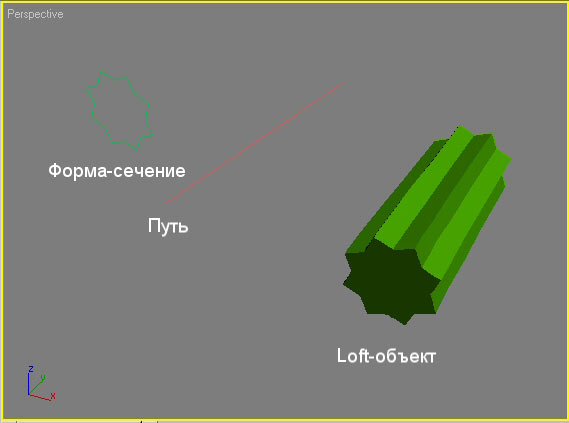
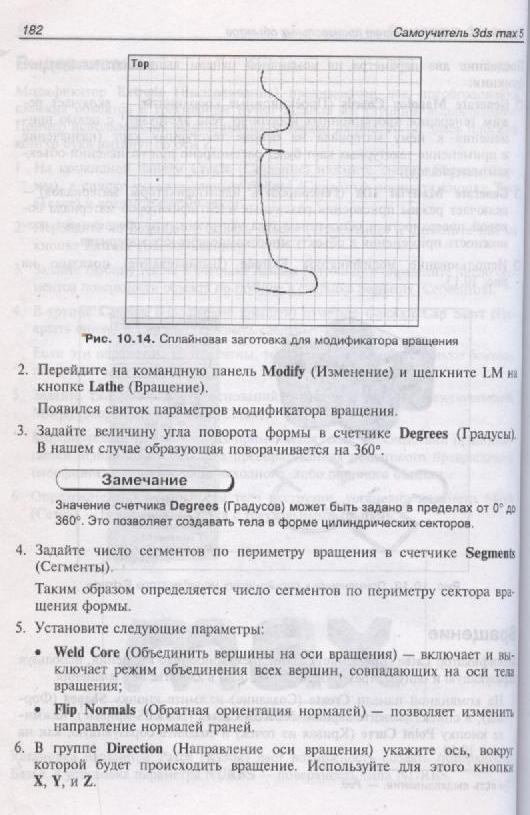
Кривые линии.

VERTICES

A point is a zero-dimensional (0D) object in 3D space. It has a set of coordinates to define

its location but has no length, width, or height. It is nothing more than a location in

Cartesian space. However, we can connect points to create edges or polylines. An edge is

part of a polygon between two vertices, and a polyline connects two vertices together that

are not part of a polygon. At its root, 3D modeling consists of nothing more than

connecting a series of vertices together to create 3D objects.

A group of vertices used to define a 3D object is called a point cloud. Each point in a cloud

is usually called a vertex and is used to define one of the corners of a polygon. Points used

to define a spline (see below) are called control points. We’ll define these terms a little

later.

SPLINES

Splines are lines that are defined  by multiple control points.
 

The

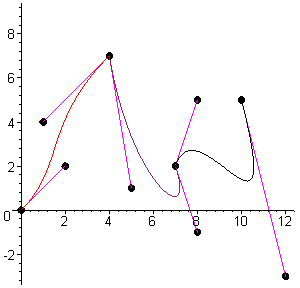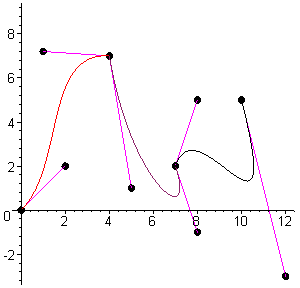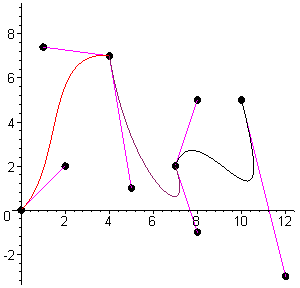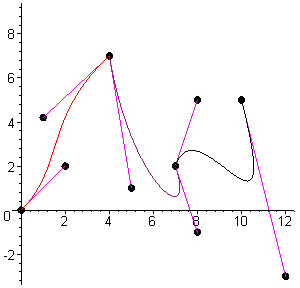
following graphic shows three  basic types of splines. The

simplest type of spline consists

of a set of control points

connected by straight lines,

called a linear spline (shown on

the near right). The other two

splines are curved. You can curve a spline by adjusting its basis, or method used to

compute the spline. Splines can be divided into interpolating and approximating.

An interpolating spline will always touch the points that define it. In the above graphic,

the two splines on the left are interpolating. This gives them a more drastic skin-like bend

than approximating splines. Approximating splines, such as the rightmost example in the

above graphic, have a softer curve because they don’t necessarily touch the points that

define them. Either type of spline requires three or more control points in order to show

any curvature. Poser uses interpolating splines for such things as the Walk Designer and

the Animation palette.

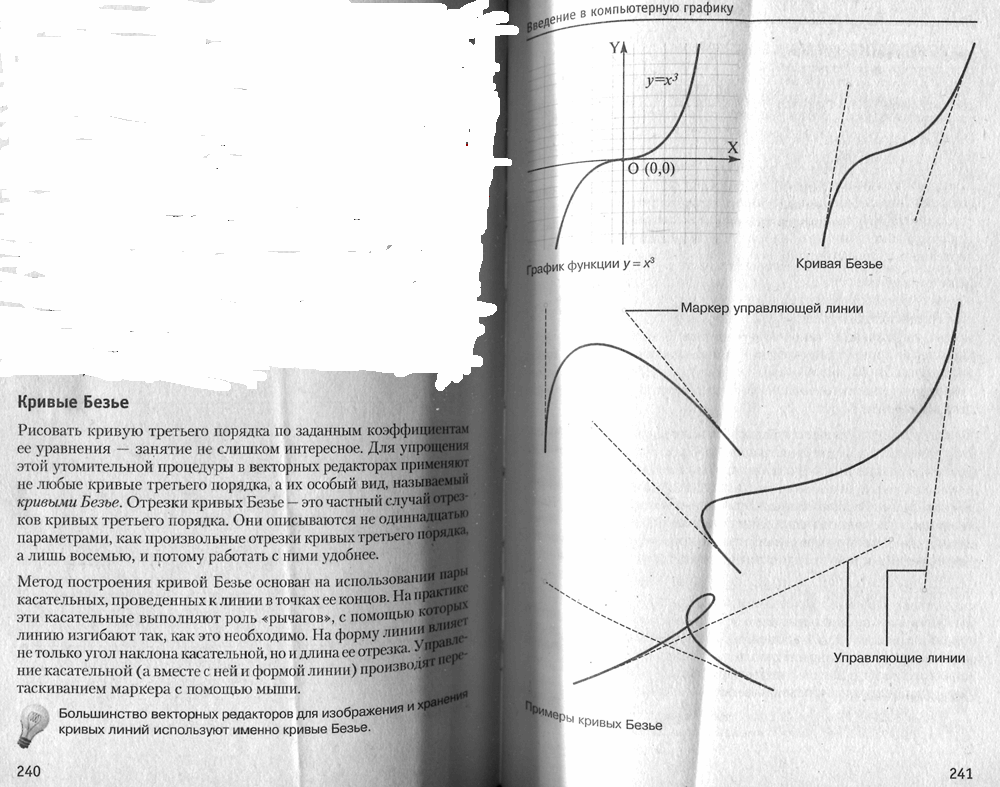
Информация получена из
Курс высшей математики-В.С.Шипачев  Москва2002

Информация получена из
Аналитическая геометрия - И.И.Привалов Москва 2005

Информация получена из
 Курс начертательной геометрии-В.Гордон М.1960

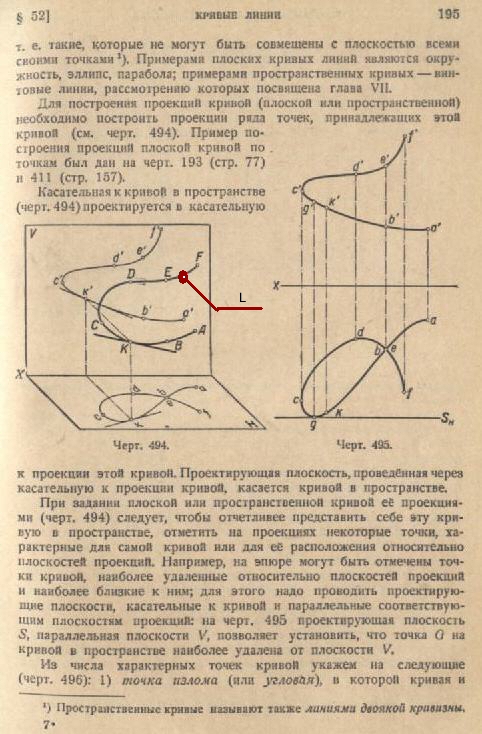
Информация получена из
 Курс черчения часть 1 -Н.С Дружинин Москва 1961

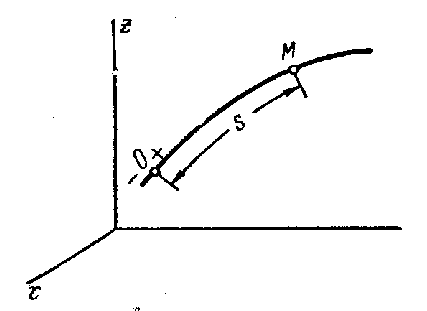
Инфомация получена
Лекции по высшей математике А.Д. Мышкис Москва

Часто встречающиеся поверхности задаваемые уравнениеями  явного вида  z=f(x,z)

Поверхность и линии в пространстве
 

Это сильное утверждение.

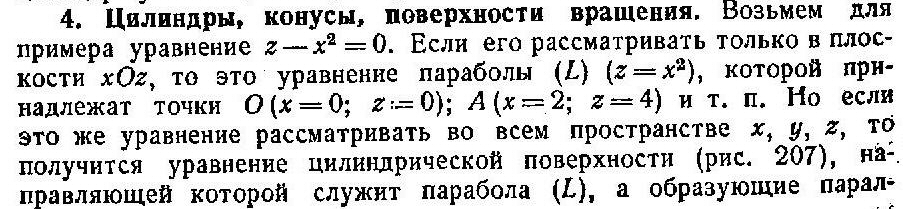
Цилиндры ,конусы ,поверхности  вращения.
Пусть имеется уравнение уравнение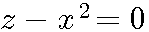  
 Если его рассматривать только вплоскости xOz ,
 
 то это уравнение параболы  (L)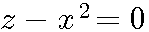    

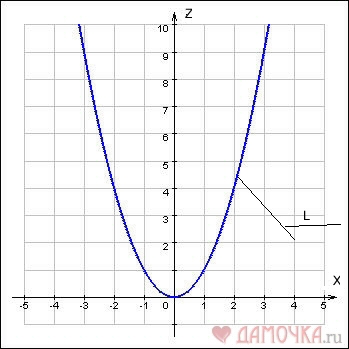
 Если   рассматривать этоже уравнение во всем пространстве x,y,z

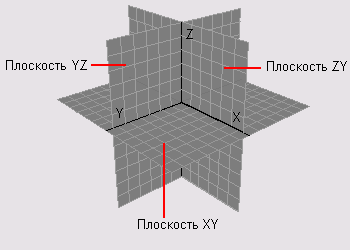
то получается уравнение целиндрической поверхности

направляющей которой служит парабола (L) , абразующей  паралельны оси y (параболический целиндр)

Shapes(формы)   в 3D MAX