Определение траектории движения точки по заданным силам

(вторая задача динамики материальной точки)

.Свободное движение материальной точки

Материальная точка брошена в пустате с начальной скоростью Uo

под углом α к горизонту.

Найти траекторию движение этой точки ,происходящее под действием только силы тяжести

Алгоритм решения

1.Выбераем систему отсчета (систему координат)

Примем начальное положение точки за начало координат ,

ось Z направим по вертикали вверх , а ось у - по горизонтали

так,чтобы начальная скорость Uo лежала в плоскости

Ozy.

2.Записываем начальное условия движения точки

Так как на точку действует только сила тяжести , то ука-

занном выборе осей имеем:
X=Y=0

Z=-mg

Кроме того,в начальный момент при t=0 имеем:

3.Составить дифференциальное уравнения движения в избранной системе отсчета:

или ,сокрощая на m:

4.Определяеме прозвольные постоянные и уравнение движения точки для выбронной системы коорднат

4.1 Определяем прозвольные постоянные и уравнение движения точки для X коорднаты

Интегрируем уравнение ,

находим :

заменя

через

тоесть проекция скорости на ось x имеет постоянное значение.

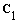
так как проекция скорости

остается неизменной , то во все время движения она имеет то же

значение , какое она имеет в начальный момент.Отсюда следует ,

что

а потому

откуда находим :

но в начальный момент X=Xo следовательно ,

Итак ,находим решение первого уравнения:

откуда следует ,что траектория точки лежит в вертикальной плоскасти

0xz

4.2 Определяем прозвольные постоянные и уравнение движения точки для Y коорднаты

Интегрируем уравнение

получаем:

тоесть проекция на ось у останеться постоянной.Также как и в предыдущем

случае ,находим ,что

Интегрируя это уравнение,получаем,

Подставляя сюда для определения постоянной

начальные значения

и

Итак ,находим решение второго уравнения:

Переходим к третьему дифференциальному уравнению

Интегрируя ,находими :

Для определения постоянной С5 нужно обратиться снова к начальным

условиям задачи; подстовляя начальные значения

и

Следовательно,

откуда ,интегрируя еще раз ,имеем :

под ставляя сюда нычальные значения

находим

Итак ,находим решение третьего уравнения:

5. Суммируем уравнения искомого движения точки в плоскости

Оxz в конечном виде

Произвольн ые постоянные ,появляющийся при интегрировании

дифференциальных уравнений движения,

определяется по начальным условиям.