Функция ,выполняемая элементом в системе называется
функциональной схемой.
Система простых логических функций, на основе которой, можно получить
любую логическую функцию, называется функционально полной. Функционально
полными, например, будут следующие пять систем
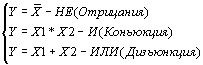
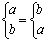
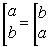
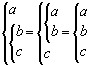
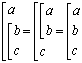
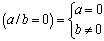
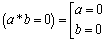
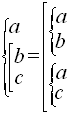
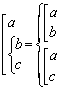
Если мы владеем правилом
(алгоритмом),по которому может быть вычислено любое значение функции
Xn и указано значение n ,То
Функция Xn считается заданной(вычисляема).
Обычный случай-это тот,когда Xn
задается формулой ,устанавливающей ,какие аналитические операции надлежит
произвести над переменным натуральном числом n (и
над постоянным ),чтобы получить соответствующие
значение функции.
Пример:
Если каждому натуральному числу n
поставлено в соответствие число Xn, То говорят , что
дана числовая последовательность
X1,X2,X3.......Xn....,XN,.....
Если N>n то То значение XN
следует за
Xn(Xn предшествует
XN) независимо от
того будет ли само число XN больше ,меньше или
даже равно Xn.
Например
Если Xn=1 то
1(1),1(2),1(3),1(4),1(5),1(6).....
постоянная величина: все "множество"
принимаемых ею значений сводится к одному.
Если
то
1(1),-1(2),1(3),-1(4),1(5),-1(6)
Множество состоит из двух значений ,принимаемых поочередно.
Если
то
0(1),1(2),0(3),1/2(4),0(5),1/3(6)
Множество имеет различные значение.
Основное свойство последовательности
Для элементов последовательности
установлен определенный порядок.
Для приближенного решения задачи
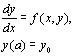
на интервале [a,b] может быть
представлена общей формы
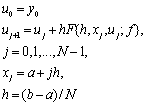
Здесь через 
обозначена
некоторая величина,чье значение однозначно
определяется величиной 
и функцией
f
Предложениями и замечаниями обращаться по адресу- vova1001@yandex.ru
