
Метод узловых напряжений (потенциалов)
Задачу анализа разветвленных цепей можно значительно упростить,если воспользоваться специальными методами, предназначенными для расчета сложных цепей.
Одним из таких методов является метод узловых на-пряжений.
В методе узловых напряжений независимыми переменными являются напряжения узлов цепи относительно выбранного базисного (опорно-го) узла.
Эти величины называют узловыми напряжениями.


Если принять потенциал базисного узла равным нулю, то узловые напряжения будут равны потенциалам соответствующих узлов.
Поэтому методназывают также методом узловых потенциалов.
Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю.
Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i1 и i2.
Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i1-i2=0.
Ток i как бы растекается на два тока поменьше и равен сумме токов i1 и i2 i=i1+i2.
Но если бы, например, ток i2 входил в узел, тогда бы ток I определялся как i=i1-i2. Важно учитывать знаки при составлении уравнения.

Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла,
т.е. электрический заряд в узле не накапливается и не исчезает.

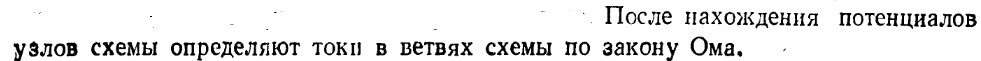








При этом, потенциал одного из узлов цепи принимается равным нулю, что позволяет сократить число уравнений до n-1.
Рассмотрим пример
![]()
|
|
|
 |
1.Пронумеруем узлы
1. Выбираем базисный узел.


Удобно выбирать заземленный узел.
|
|
 |
 |
или узел, в котором сходится наибольшее число ветвей.
Примем узел 1 за базовый и будем считать его потенциал равным нулю.
|
|
 |
2 - расставим токи в ветвях (от предполагаемого узла с большим потенциалом к меньшем
|
|
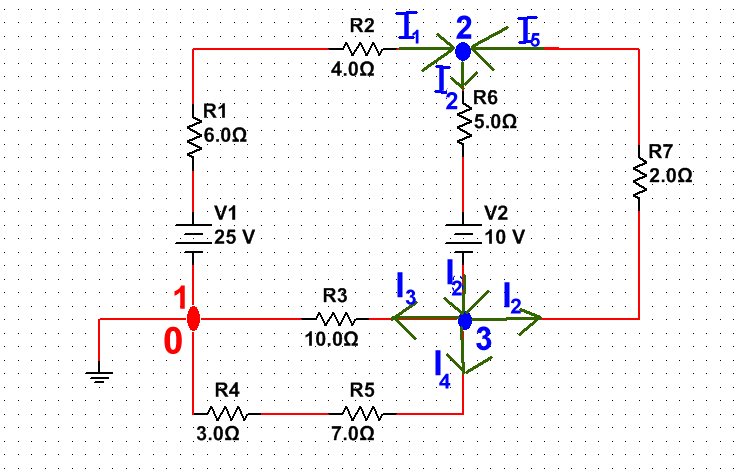 |
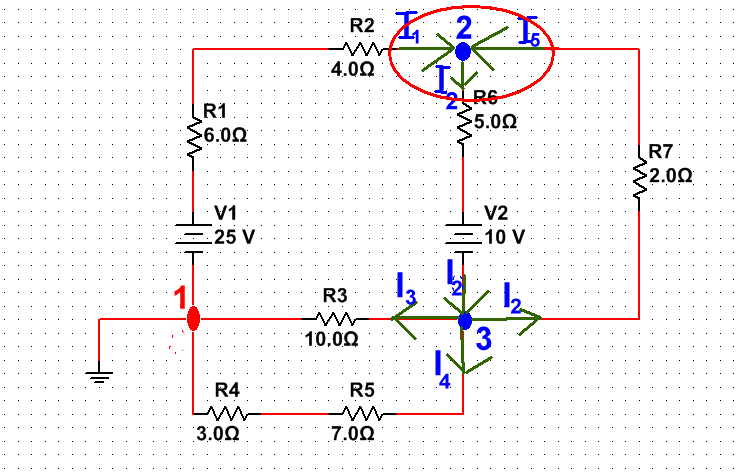
Составим уравнения по первому закону Кирхгофа для узла 2,3 (для узла 1 не составляем, так как это не требуется)
|
|
|
 |
|
|
|
|
3-акона Ома
Запишем выражения закона Ома для различных участков цепи, приведенных на рисунке 2.26

Рисунок 2.26. – Закон Ома: а) с источником напряжения;
б) без источника напряжения
Для участка цепи, содержащего источник напряжения
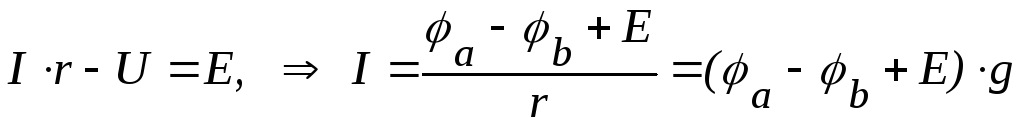
Для участка цепи, не содержащего источник напряжения:

Составим уравнения для нахождения каждого из токов
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
Получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 – Подставим полученные выражения для токов в уравнения из пункта 2, получим
|
|
|
|
|
|
Прочитать статью
http://vova1001.narod.ru/Substitute.htm


Получим


Приведение подобных слагаемых

Прочитать статью
http://vova1001.narod.ru/Collect.htm

Подставляем значение u2 в


Решаем уравнение

Подставляем значения

Получим


![]()


|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |


|
|
|




