Свободный(собственный) колебательный в контур.

The algorithm

Step 1
The mathematical formulation of the data

Колебания в контуре получаются без какого либо внешнего воздействия называются  
свободными или собственными колебания контура.

Составить уравнение наприжения конденсатора(Uс) колебательного контура.

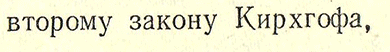
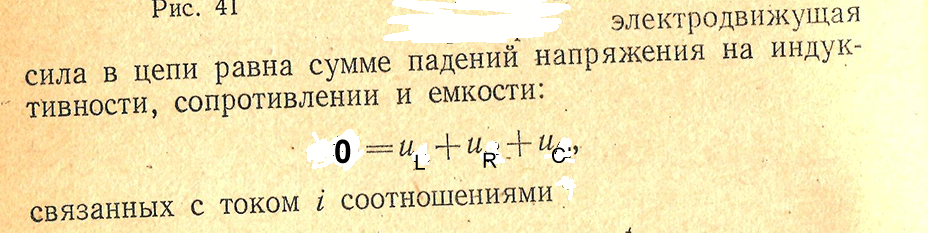
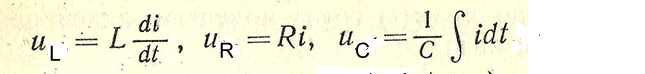
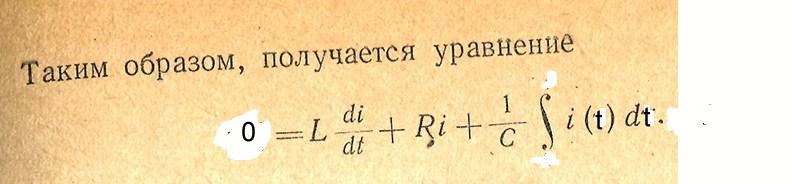
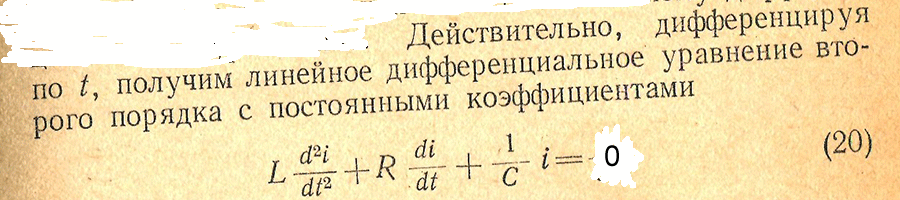
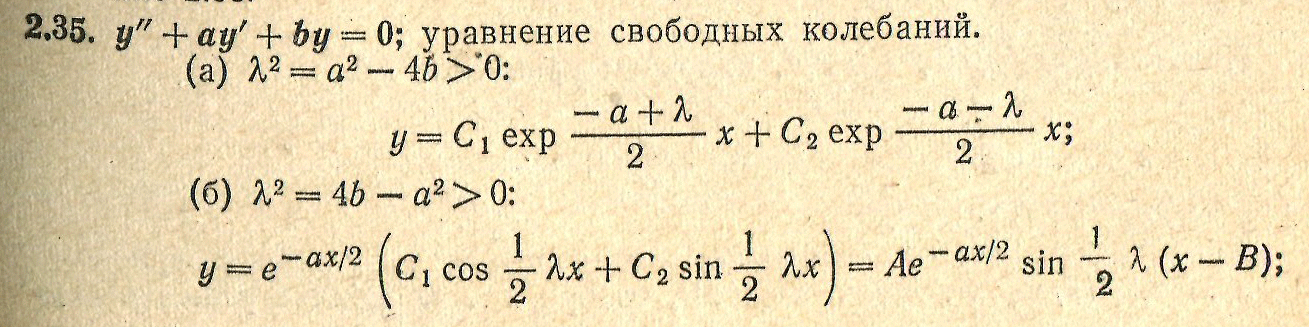
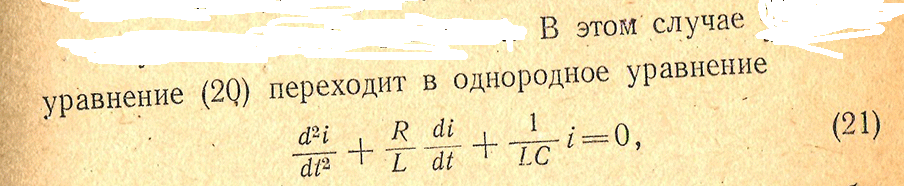
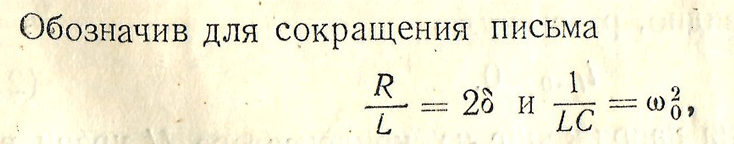
Получим

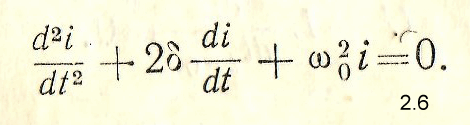
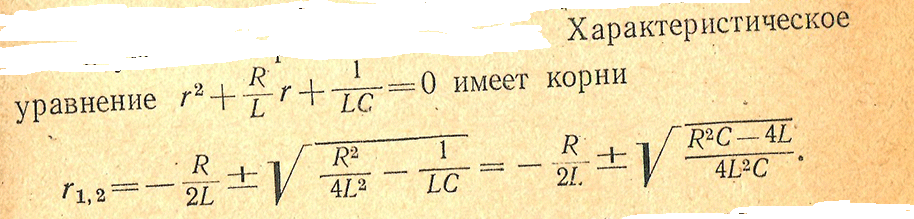
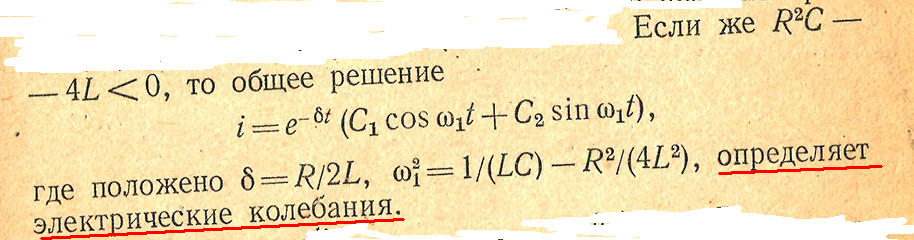
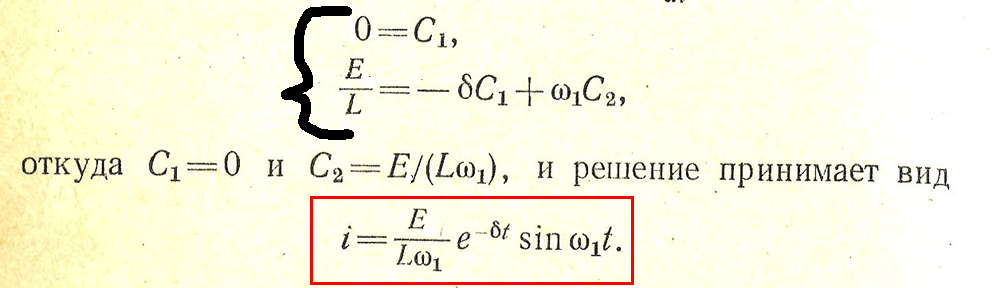
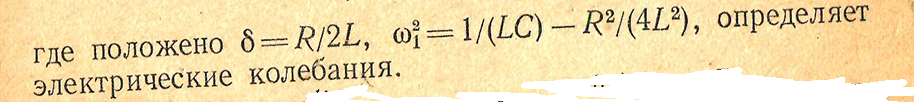
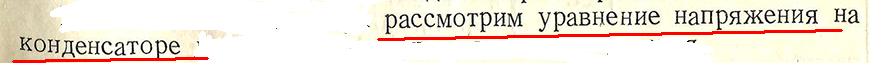
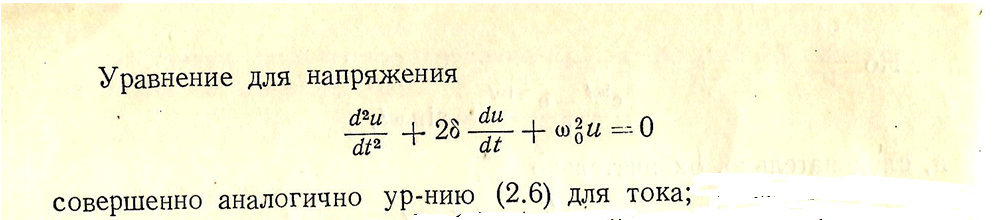
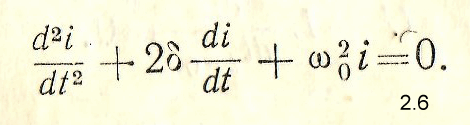
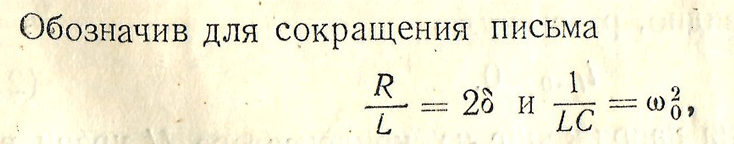
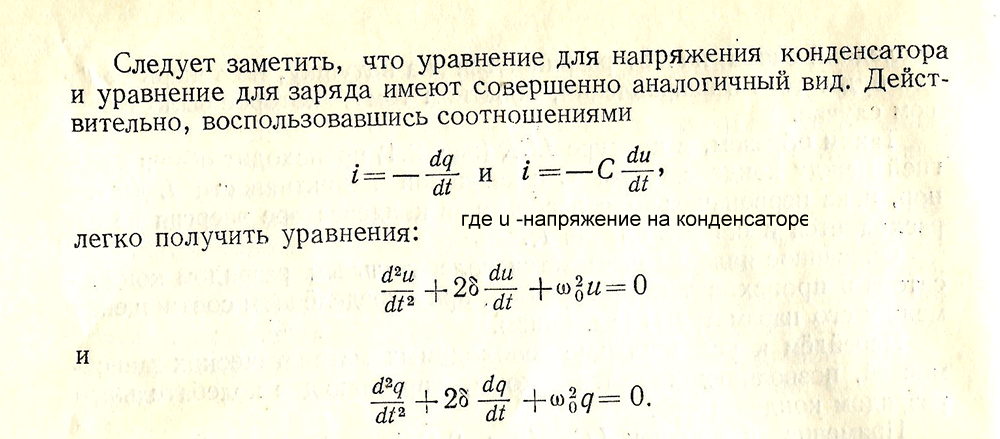
следовательно , решение будет аналогичное

Колебание создаёт волну.

Гармоническое колебание

В реальных системах колебания по прошествии некоторого времени затухают из-за диссипации энергии.

Таким образом, представлением о гармонических колебаниях можно пользоваться лишь для времен, малых по сравнению с характерным временем затухания.
Затухание реальных  системах колебаний всегда будет наблюдаться  с сопротивлением.
 

Step 2

Verification of theoretical data

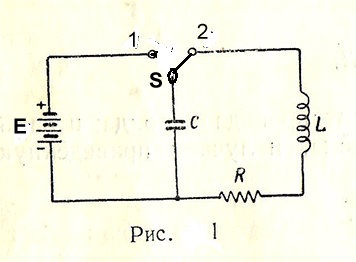
Теаретическая установка создания  свободного(собственного) колебания.

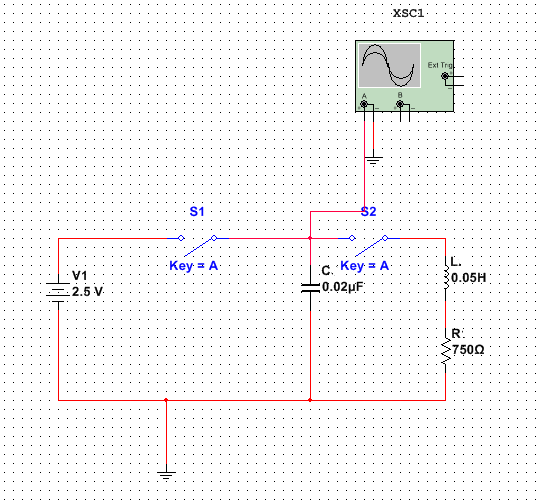
1 Шаг
Включим переключатель S1
 тогда
конденсатор будет подлючен к источнику и зарядится до наприжения , котрое имеется на его зажимах

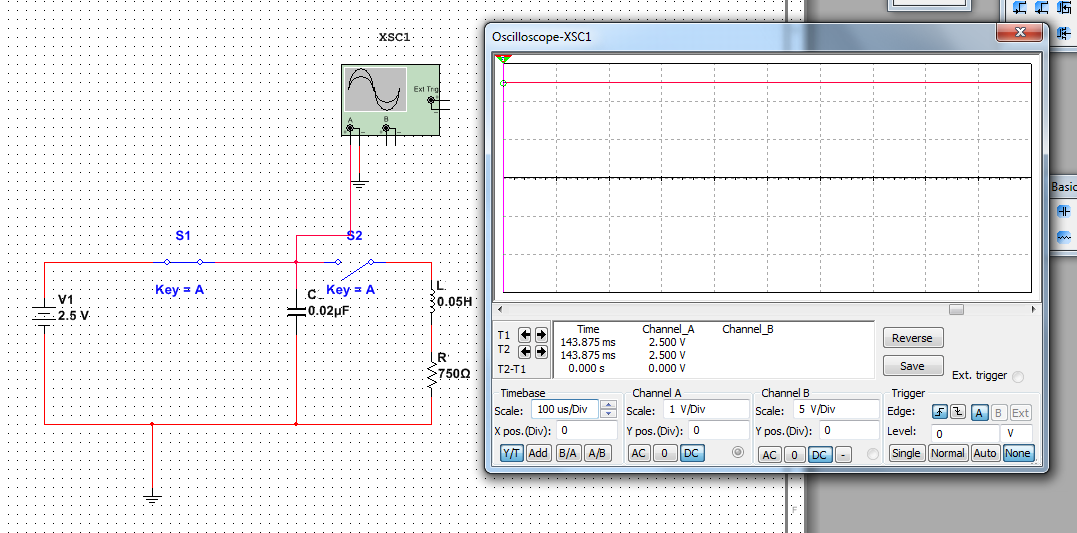
2 Шаг
Отключимчим переключатель S1 и включим переключатель S2

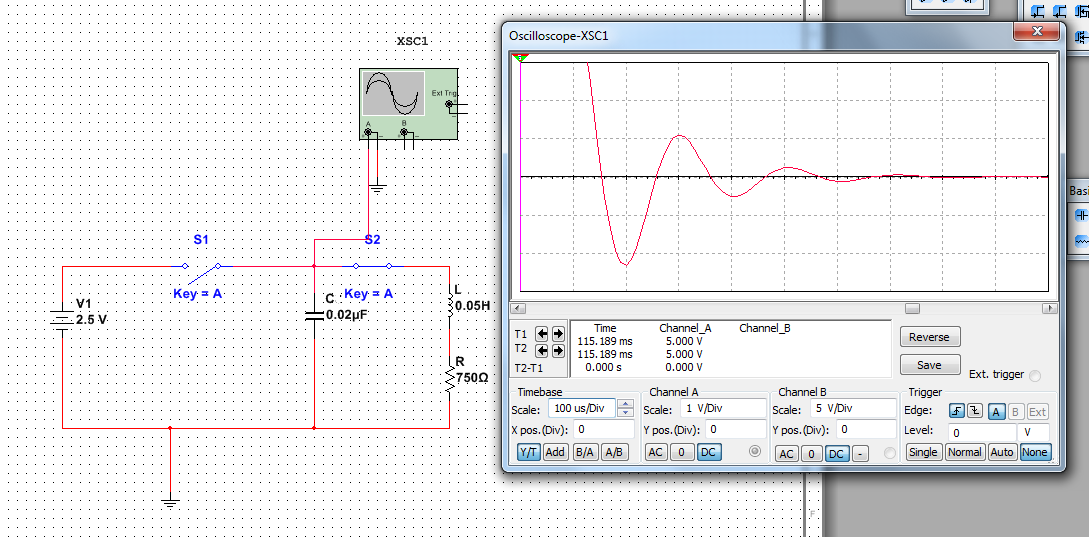
Идеальный контур  R =0

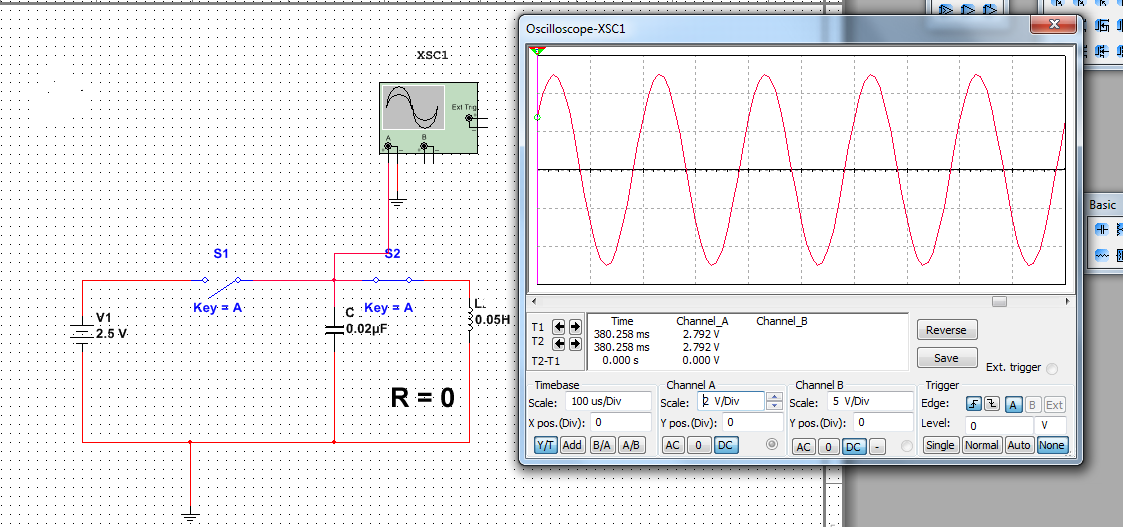
Step 3

Verification  of experimental data

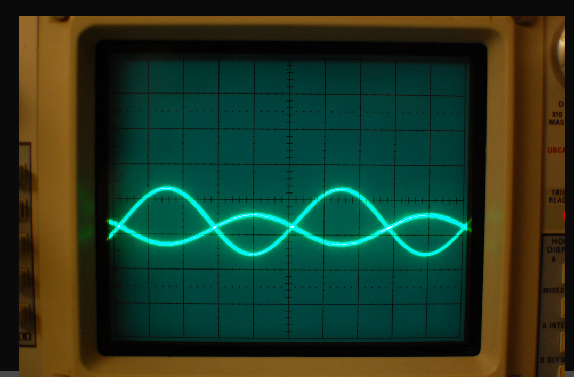
Чтобы наблюдать(исследовать) с  помощью непрерывной развертке периодическую затухающие гармоническое колебание  
используется прямоугольные импульсы.

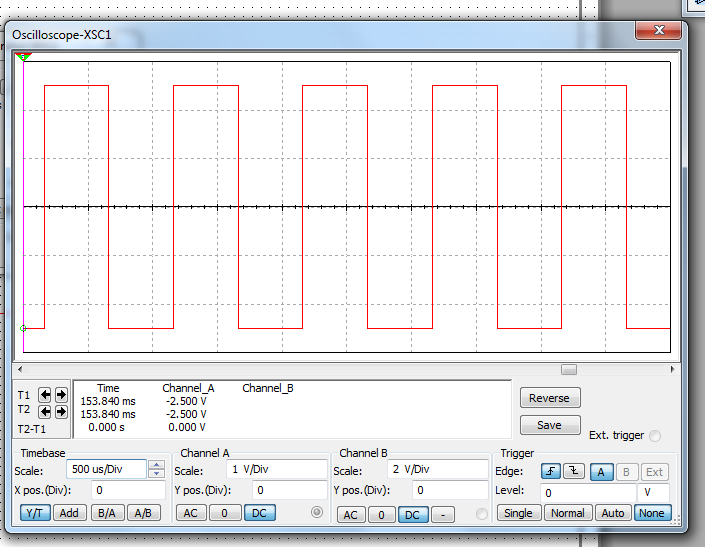Теоретическая эксперементальная устновка

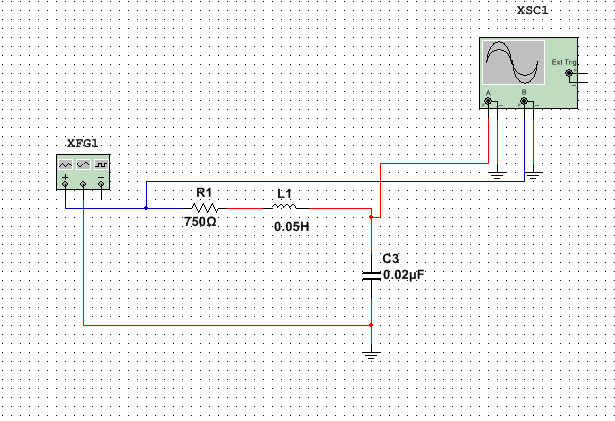
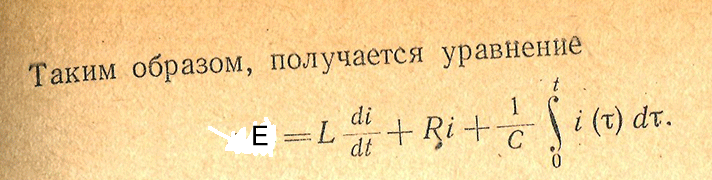
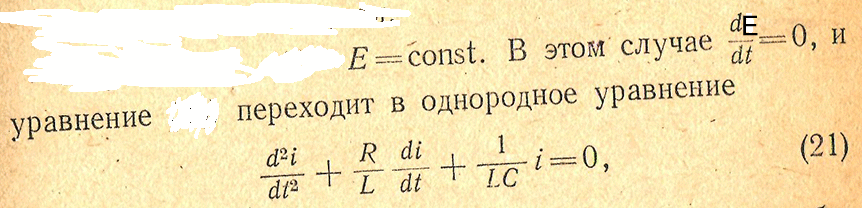
Смотри  теоретическое решение
 Step 1
The mathematical formulation of the data

Результат

Результат  эксперемента